
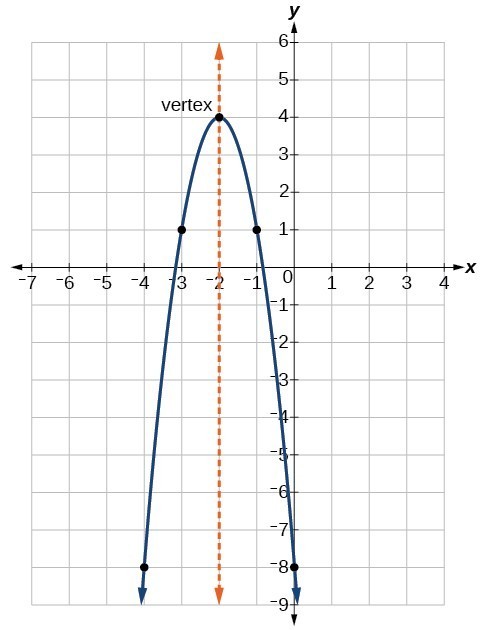
Then read more about the Quadratic Equation. Also see the 'roots' (the solutions to the equation). The Quadratic Formula Calculator finds solutions to quadratic equations with real coefficients. The roots of the equation \(y = x^2 -x – 4 \) are the x-coordinates where the graph crosses the x-axis, which can be read from the graph: \(x = -1.6 \) and \(x=2.6 \) (1 dp). A Quadratic Equation ( a, b, and c can have any value, except that a cant be 0.) Try changing a, b and c to see what the graph looks like. Step 1: Enter the equation you want to solve using the quadratic formula. Plot these points and join them with a smooth curve. Exampleĭraw the graph of \(y = x^2 -x – 4 \) and use it to find the roots of the equation to 1 decimal place.ĭraw and complete a table of values to find coordinates of points on the graph. When the graph of \(y = ax^2 + bx + c \) is drawn, the solutions to the equation are the values of the x-coordinates of the points where the graph crosses the x-axis. If the equation \(ax^2 + bx + c = 0 \) has no solutions then the graph does not cross or touch the x-axis. If the equation \(ax^2 + bx + c = 0 \) has just one solution (a repeated root) then the graph just touches the x-axis without crossing it. If the graph of the quadratic function \(y = ax^2 + bx + c \) crosses the x-axis, the values of \(x\) at the crossing points are the roots or solutions of the equation \(ax^2 + bx + c = 0 \). You can also graph quadratic functions by applying transformations to the graph of the parent function f(x) x2. Graph of y = ax 2 + bx + c Finding points of intersection Roots of a quadratic equation ax 2 + bx + c = 0 We have found 16 NRICH Mathematical resources connected to Quadratic functions and graphs, you may find related items under Coordinates, Functions and. The turning point lies on the line of symmetry. The graph of the quadratic function \(y = ax^2 + bx + c \) has a minimum turning point when \(a \textgreater 0 \) and a maximum turning point when a \(a \textless 0 \).
#Quadratic graph full
Problems with full solutions, more problems with answersĪ simplified and updated version of the classic Schaum's Outline.All quadratic functions have the same type of curved graphs with a line of symmetry. What key features of a quadratic graph can be identified and how are the graphs affected when the.

The classic algebra problem book - very light on theory, plenty of Click here to get an answer to your question 4. Will save a great deal of trouble later, and will probably serve you very well in your The ability to go from an equation toĪ graph and vice-versa is literally an indispensable skill. Math, chemistry, physics, business and engineering. Graphing skills are extremely useful and are constantly used in more advanced

This is one area in particular where it really pays to do a very large number of So our final answer, the quadratic form, comes out to be Now we have all the graphical form constants, we can just plug into the conversion We still need the amplitude, so let's take one of the points, say (0, 0), and plug Since the vertex is clearly at (-1, -1), it seems clear that x 0 = -1 and y 0 ItĪppears that we can identify three points on the graph: See what we think we see and avoid getting too technical about the points on the graph. This type of problem is best done "naively", that is, let's assume that we Looking at this graph, find the standard quadratic form for the equation. If you like, you can plot three points: x = 1 => y = 1, x = 0 => y = 3 and x = 2 However, if I restrict their domain to where the x x x values produce a graph that would pass the horizontal line test, then I will have an inverse function. (1, 1) which is skinny compared with a "normal" parabola (a = 2 instead of a =ġ). The cup is upright (vertex down) when a > 0, upside down (vertex up) when a 0) with vertex at (x 0, y 0) = Interested in the region around the vertex. The mouth of the cup keeps getting larger to infinity. The graph looks a little like a cup, and the bottom of the cup is called the vertex. Quadratics and the Quadratic Formula: Theory and GraphingĮvery quadratic equation describes a parabola, which looks like this graph. Of the Rings DVDs, Videos, Books, Audio CDs and Cassettes ĭVDs, Videos, Books, Audio CDs, Audio Cassettes and Toys
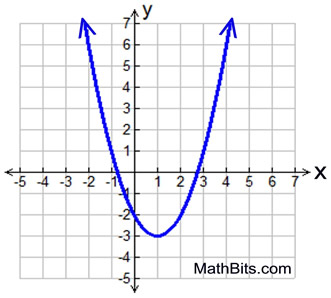
Potter DVDs, Videos, Books, Audio CDs and Cassettes What are quadratic graphs Quadratic graphs are graphs of quadratic functions that is, any function which has x2 x2 as its highest power. Math Help - Algebra - Quadratics - Theory - Graphs


 0 kommentar(er)
0 kommentar(er)
